SANTOS LÓPEZ LEYVA
A mediados del mes de abril de 1971, una tarde me encontraba jugando basquetbol en la cancha de la escuela primaria Agustina Ramírez de Guamúchil Viejo, cuando este poblado estaba separado de Guamúchil, hasta allí llegó el profesor Celestino Martínez de la Rosa, quien en ese momento era dueño del Colegio Insurgentes, una escuela secundaria particular. Yo ya había terminado mi primer año de la especialidad en matemáticas en la Escuela Normal Superior “José E. Medrano”, ubicada en Chihuahua, Chihuahua. El profesor Celestino me invitó a dar clases en un tercero de secundaria grupo nocturno, en sustitución del profesor Federico Crispín Antúnez, quien era mi compañero en la misma escuela Agustina Ramírez. Empecé mi carrera de maestro de secundaria con ese grupo, les impartí la clase de trigonometría, estos alumnos, al siguiente semestre,serían mis compañeros en la preparatoria nocturna de Guamúchil.
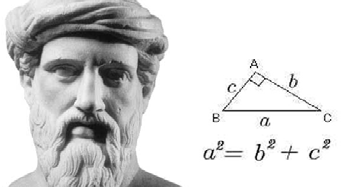
Un agravio a Pitágoras
En enero de 1974, hice mi cambio a la ciudad de Culiacán, a la escuela primaria Ramón F. Iturbe, que en ese tiempo estaba dentro de la Novena Zona Militar, solicité ese cambio porque ya había empezado a estudiar economía, y desde septiembre de 1973, Regino López Acosta y un servidor viajábamos a diario de Guamúchil a Culiacán, él estudiaba en la Escuela Libre de Derecho y yo en la Escuela de Economía de la Universidad Autónoma de Sinaloa.
Al siguiente año, 1975, empecé a trabajar como maestro de matemáticas en una escuela particular en Culiacán, impartía la materia de álgebra en un segundo de secundaria y trigonometría en un tercero. En el tercer grado habíamos dos profesores, pero el director me encomendó elaborar el examen final de trigonometría. Una pregunta obligada del examen era: calcule las funciones trigonométricas de un triángulo rectángulo si su seno es igual a 3/5. El día y hora del examen me llamaron de la dirección, allí estaba el otro maestro y su reclamo era que no se podía resolver el problema porque no se tenía el valor del otro cateto. Sin ninguna protesta ni asombro le dije que el otro cateto tenía un valor de 4, y se fue contento a informar al grupo para que siguieran resolviendo el examen.
Me quedé pensando y hasta ahora me resisto que eso fuera cierto, porque, sin duda, ese es un atropello al talento de Pitágoras, que un profesor de trigonometría no conociera su teorema que expuso 25 siglos antes el genio de Samos. Aunque se dice que lo trajo de Egipto.
En un triángulo rectángulo el cuadrado construido sobre la hipotenusa es igual a la suma de los cuadrados construidos sobre los catetos. Matemáticamente se expresa:
C² = a² + b²
En el problema presentado el valor de C=5, que es la hipotenusa y el valor de a=3, que es cateto opuesto, sólo había que despejar el valor de b, o sea, el cateto adyacente, que al hacer el despeje tiene un valor de 4, ya con ello se puede encontrar el valor de todas las restantes funciones trigonométricas.
México en el campo de las matemáticas
México, aunque nuestros antepasados, en manera precisa, los mayas y toltecas fueron excelentes matemáticos y astrónomos, en la actualidad no presenta buen desempeño en esta disciplina.
Al revisar los resultados de 2015, todavía no aparecen los de 2018, del Programa Internacional de Evaluación de Estudiantes (PISA, por sus siglas en inglés), de la Organización para la Cooperación y el Desarrollo Económicos (OECD), se encuentra que los estudiantes de tercero de secundaria alcanzaron 408 puntos, o sea 154 puntos por abajo de los estudiantes de Singapur que lograron 564 puntos, atrás también de Chile que logró 423 puntos y Uruguay 418. No se observa una mejora considerable en este campo, pues en 2006, la calificación fue de 406 puntos, 143 puntos por debajo de China Taipéi que logró 549 puntos. Con estos resultados, nuestros jóvenes de 15 años, presentan dos años de retraso en escolaridad con respecto a los jóvenes de Singapur.
Por otra parte, el Foro Económico Mundial en 2017 ubicó a México en el lugar 117, de 137 países que estudió, en enseñanza de matemáticas y ciencias, siendo el número 1 el mejor país y el 137, el peor. O sea que sólo 20 países de los estudiados estaban peor que México en este campo. En educación primaria nos calificaron en el lugar 114 también una posición nada envidiable.
Lo anterior indica que México debe mejorar sus métodos pedagógicos en la enseñanza de las matemáticas y de las ciencias en general; debe existir una mayor preocupación por la preparación de los maestros, de mejorar la estructura física de las escuelas, perfeccionar los materiales didácticos y en general, reformar la dimensión institucional de la educación básica. Con todo ello, transformar el proceso de enseñanza aprendizaje de los estudiantes con la finalidad de remontar en los indicadores de evaluación de este nivel educativo.

*Profesor de la Facultad de Economía y Relaciones
Internacionales de la Universidad Autónoma de
Baja California,Tijuana, Baja California

